Understanding the Pauli Exclusion Principle in Simple Terms
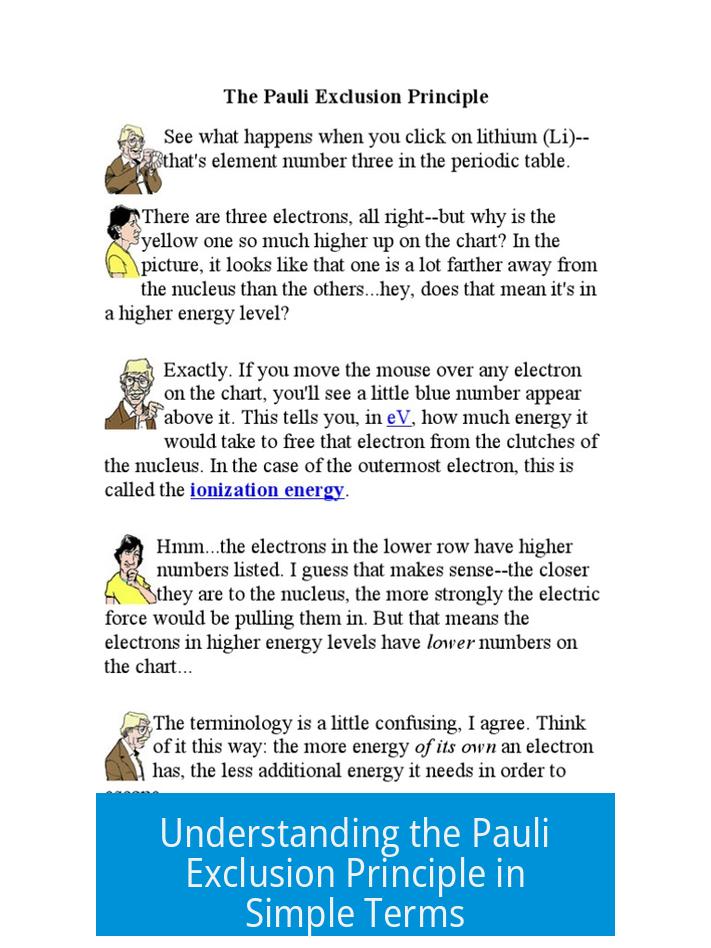
The Pauli Exclusion Principle states that no two electrons in an atom can have exactly the same set of quantum numbers, which means no two electrons can occupy the identical quantum state simultaneously. This principle applies not only to electrons but all fermions, particles like protons and neutrons, that follow this quantum rule.
What Does “Quantum State” Mean?
Every electron in an atom is described by four quantum numbers:
- Principal quantum number (n): energy level
- Angular momentum quantum number (l): shape of orbital
- Magnetic quantum number (m): orientation of orbital
- Spin quantum number (s): electron’s spin direction, either +1⁄2 or -1⁄2
No two electrons can share all four numbers simultaneously. At least one must be different, which keeps electrons unique within an atom.
Role of Spin: The Key Difference
When electrons occupy the same orbital (same n, l, m), the only difference allowed by the exclusion principle is their spin. For example, in a single orbital, one electron has spin +1⁄2 (often pictured as “arrow up”) and the other -1⁄2 (“arrow down”).
This difference in spin allows two electrons to coexist in the same orbital but not in the exact same quantum state.
Mathematical Interpretation: Antisymmetric Wavefunctions
The principle also has a quantum mechanical explanation using wavefunctions. Electrons are described by wavefunctions that depend on their positions and spins.
“The Pauli Principle requires that wavefunctions for fermions be antisymmetric under exchange.”
Mathematically, swapping two electrons flips the sign of the wavefunction:
F(e1, e2) = −F(e2, e1)
This antisymmetric property means if two electrons tried to occupy the exact same state, the wavefunction would be zero, implying zero probability of that arrangement. Hence, it’s forbidden.
Physical Effects of the Pauli Exclusion Principle

The principle rocks atomic and macroscopic worlds:
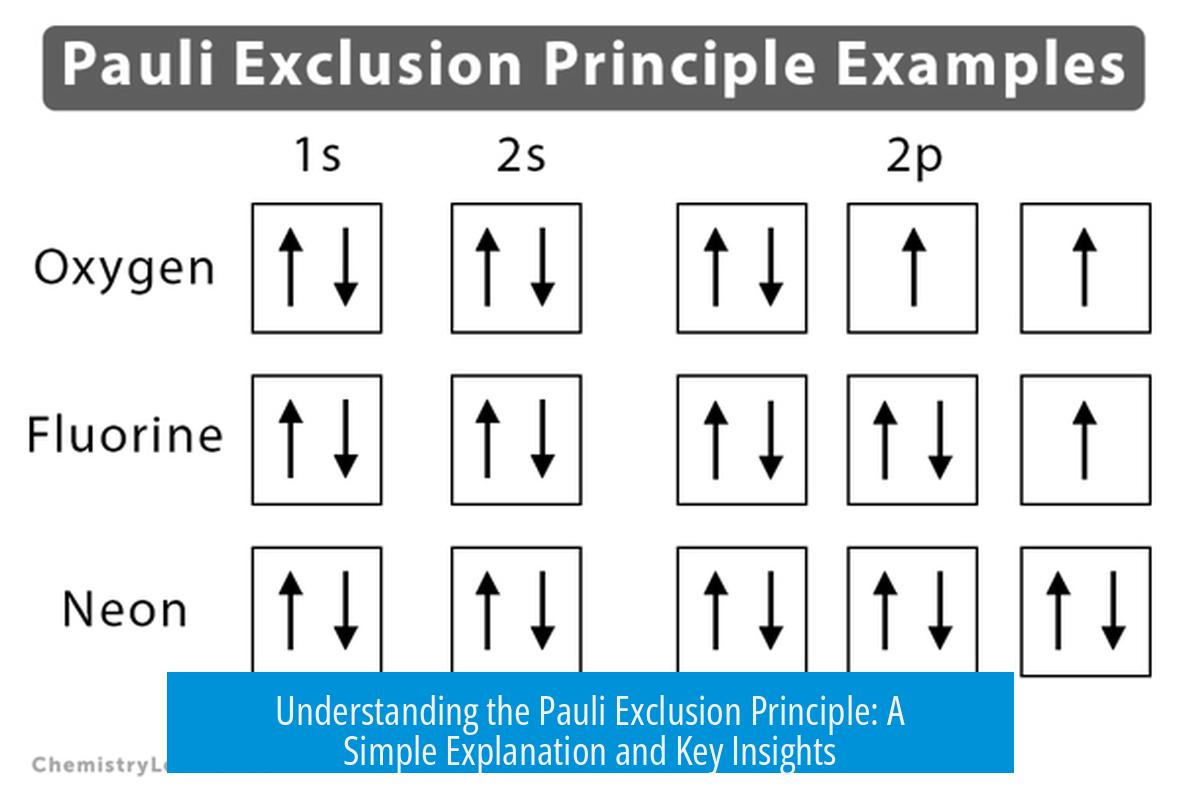
- Electron arrangement in atoms: It explains why electrons fill orbitals one by one, building the structure of the periodic table.
- Virtual repulsion: Pauli creates a kind of effective force that makes similar electrons avoid each other beyond just their electrical charge.
- Macroscopic stability: This principle supports the stability of matter, preventing electrons from collapsing into the nucleus.
- Astrophysical importance: It generates degeneracy pressure in dense stars like white dwarfs and neutron stars, stopping gravitational collapse.
Simple Analogies
One helpful analogy is a parking lot:
- Imagine an orbital as a tiny parking lot with two slots.
- Each slot must be occupied by a car parked differently—one forward, one reversed.
- No two cars can occupy the same slot or park facing the same way.
- This represents electrons filling the same orbital with opposite spins.
This analogy visually explains why electrons cannot share the same quantum state.
Common Misunderstandings
The exclusion principle is often oversimplified as “no two particles can be in the exact same place,” but it is more specific to quantum states.
It doesn’t just restrict electrons from crowding in physical space but also forbids identical quantum properties like spin direction.
Summary of Key Points
- The Pauli Exclusion Principle forbids identical fermions from occupying the same quantum state.
- Each electron is distinguished by four quantum numbers; at least one must differ between electrons.
- Spin is the main differentiator for electrons sharing an orbital, requiring opposite spins.
- Mathematically, electron wavefunctions for fermions are antisymmetric under exchange.
- The principle affects atomic structure, chemical properties, and the state of dense astrophysical objects.
- Virtual repulsion from the principle differs from electric repulsion but influences electron behavior.
What does the Pauli Exclusion Principle say about electrons in an atom?
It says no two electrons can have the exact same set of quantum numbers. Each electron must differ in at least one property, like spin, position, or momentum. This keeps them from being identical within an atom.
How does spin affect the Pauli Exclusion Principle in simple terms?
Two electrons can share the same orbital only if their spins are opposite. For example, one spins “up” and the other spins “down.” This one difference allows them to coexist in the same space.
Why is the Pauli Exclusion Principle important for matter stability?
It stops electrons from all collapsing into the lowest energy state. This creates the structure of atoms and explains why matter takes up space and doesn’t just collapse.
Can you explain the wavefunction aspect of the Pauli Principle?
Electrons are described by wavefunctions that change sign when two electrons are swapped. This antisymmetric property ensures that two electrons cannot share the same quantum state.
What is the “virtual force” created by the Pauli Exclusion Principle?
It pushes electrons with the same spin apart, not by electric force but by quantum rules. This prevents electrons from getting too close and affects the shape of molecules.




Leave a Comment