Understanding Hybridization in Molecular Orbital Theory: Key Insights and Implications

Hybridization in Molecular Orbital (MO) Theory

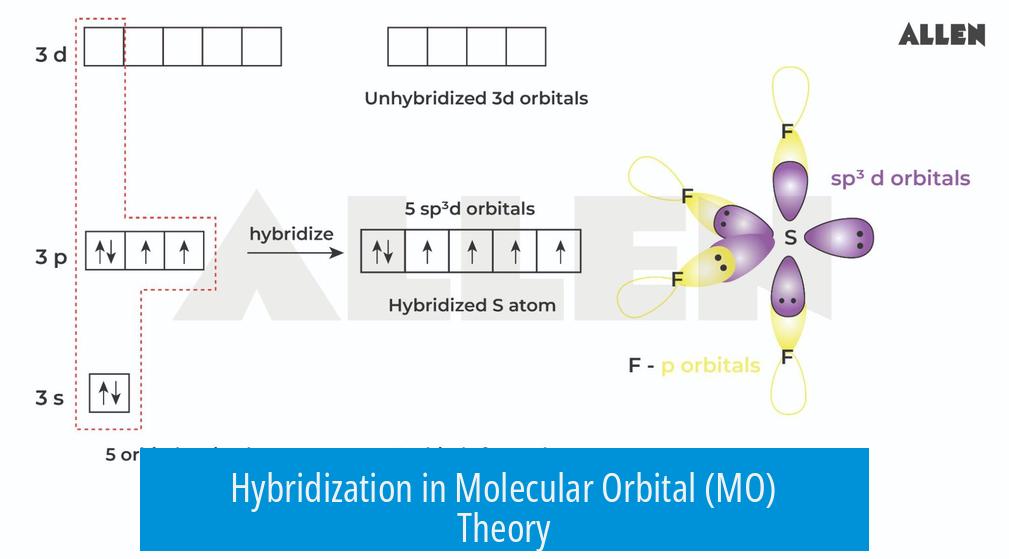
Hybridization is a concept originating from valence bond (VB) theory and does not formally exist within molecular orbital (MO) theory. In MO theory, electrons are described as occupying molecular orbitals that extend over the entire molecule rather than localized hybrid orbitals. Hybridization provides a useful structural approximation but does not represent the true behavior of electrons in molecules according to MO theory.

Understanding Hybridization and Its Origins

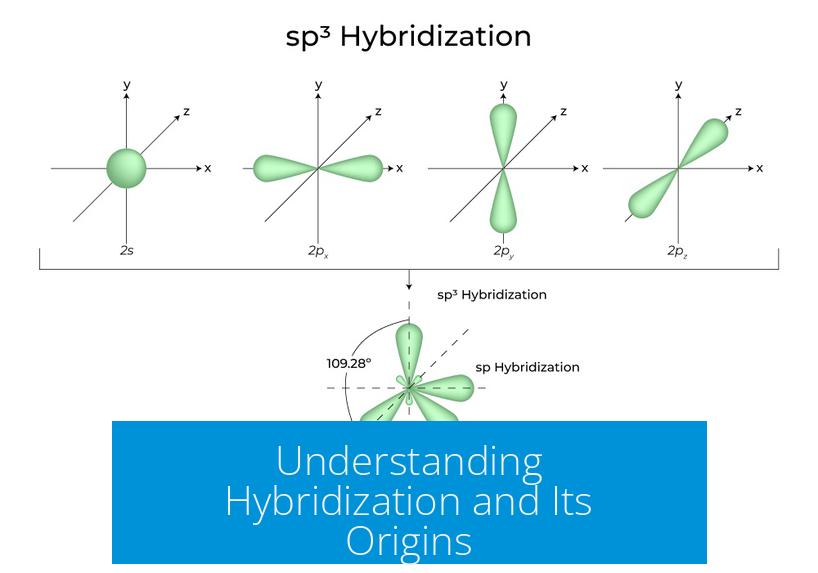
Hybridization arises from valence bond theory to rationalize molecular shapes and bonding patterns that simple atomic orbital models fail to explain accurately. It describes the mixing of atomic orbitals within an atom, producing new hybrid orbitals that have different shapes and energies.

• Hybrid orbitals form by combining nearly equal energy atomic orbitals (like s and p).
• The number of hybrid orbitals equals the number of original atomic orbitals combined.
• These hybrid orbitals are more directional, enabling better orbital overlap.
• Better overlap results in stronger bonds and more stable molecules.

For example, sp3 hybridization involves the mixing of one s and three p orbitals to generate four equivalent orbitals arranged tetrahedrally. This explains the approximately 109.5° bond angles observed experimentally in many organic compounds.

Hybridization: A Useful Approximation, Not a Physical Reality

Hybridization is widely regarded as a simplified model rather than an exact physical phenomenon. It is useful because it predicts molecular shapes and bonding qualitatively well. However, it is not “true” in a strict quantum mechanical sense.

Hybridization “doesn’t exist. It’s a useful approximation to make accurate predictions about molecular shapes and reactivity, but it is not a physical reality.”

In contrast, molecular orbital theory treats electrons as delocalized over the entire molecule, forming molecular orbitals rather than localized, directional hybrids. This better reflects the quantum reality but is computationally intensive and less intuitive for understanding shape.

Comparing Hybridization (VB Theory) and Molecular Orbital Theory

Feature	Hybridization (VB Theory)	Molecular Orbital Theory
Electron Description	Electrons occupy localized hybrid orbitals on atoms	Electrons occupy delocalized molecular orbitals spanning the molecule
Explanation of Bonding	Orbital mixing to improve bonding overlap	Linear combination of atomic orbitals to form molecular orbitals
Prediction of Molecular Shape	Good, matches experimental geometries	Poor, shape not directly predicted
Computational Complexity	Low, easy to visualize	High, more accurate but complex
Applications	Qualitative bonding and shape, common teaching model	Quantitative electronic structure, excited states, spectra

Thus, each model serves different purposes. MO theory is more rigorous and accurate for electronic properties, while hybridization excels in predicting molecular geometry simply.

Mixed Models: Huckel Molecular Orbital Theory

Hybridization ideas are sometimes incorporated into MO methods to create hybrid models. Huckel Molecular Orbital (HMO) theory is an example.

• HMO uses valence bond/hybridization concepts for sigma bonds.
• It applies MO theory to describe the pi-electron system.
• This combination extends the explanatory power beyond the simple VB/hybridization model.
• HMO accounts for conjugation, aromaticity, and excited states.

Nonetheless, HMO is less quantitative than full MO theory and cannot capture some fine phenomena, such as hyperconjugation effects.

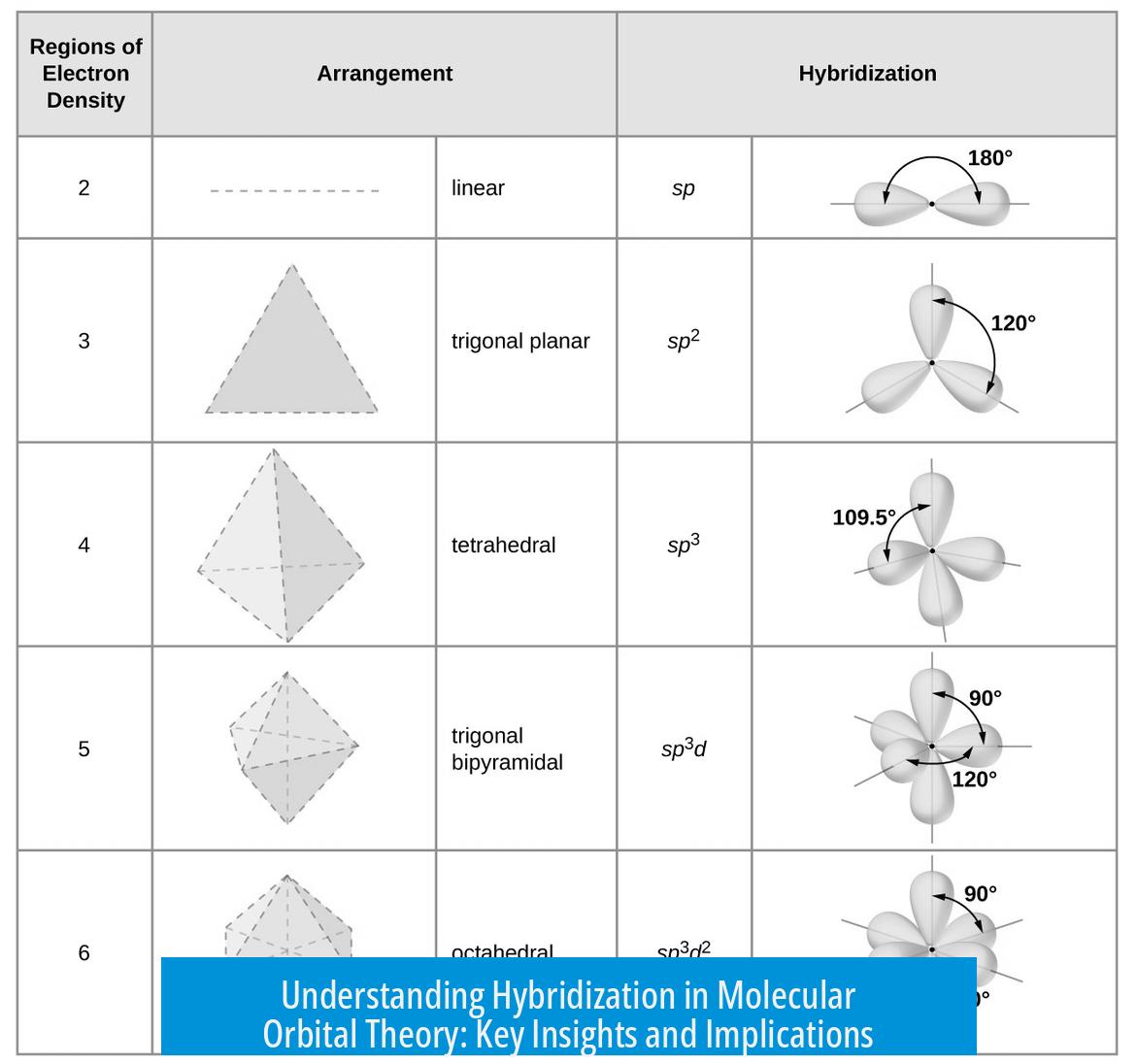
The Main Types of Hybridization

Hybridization explains common molecular geometries by combining s and p orbitals in different ratios. The key types include sp3, sp2, and sp. Each corresponds to specific molecular shapes.

sp3 Hybridization

• Mixes one s and three p orbitals (2s + 2px + 2py + 2pz).
• Forms four equivalent sp3 hybrid orbitals.
• Orbital composition: 25% s character, 75% p character.
• Geometry: tetrahedral with bond angles of ~109.5°.
• Example: Carbon in methane (CH4).

sp2 Hybridization

• Mixes one s and two p orbitals (e.g., 2s + 2px + 2py).
• Produces three equivalent sp2 hybrid orbitals.
• Orbital composition: 33% s character, 67% p character.
• Geometry: trigonal planar with bond angles of 120°.
• Examples: Carbon in ethene (C=C), aluminum in AlH3.

sp Hybridization

• Combines one s and one p orbital (2s + 2px).
• Forms two equivalent sp hybrid orbitals.
• Orbital composition: 50% s character, 50% p character.
• Geometry: linear with bond angles of 180°.
• Example: Carbon in ethyne (C≡C), magnesium in MgH2.

Why Hybridization Helps Explain Molecular Shape

Experimental evidence shows bond angles cluster around 109°, 120°, or 180° in many organic molecules. VSEPR (Valence Shell Electron Pair Repulsion) theory explains this by electron pair repulsions, causing electron pairs to spread out maximally.

Hybridization provides a model in which directional, equivalent orbitals place bonding electron density in positions accounting for these bond angles. It bridges experimental observations with an orbital-based picture.

The Energetics of Hybridization

When atomic orbitals hybridize, their energy redistributes evenly, forming hybrid orbitals of equivalent energy. This equalization allows symmetrical bonding environments and better orbital overlap.

Hybrid orbitals are more directional, favoring stronger bonds than pure s or p orbitals. This directional bonding stabilizes molecular structures.

Distinctions from Molecular Orbital Theory

Molecular orbital theory does not rely on hybridization. Instead, atomic orbitals combine linearly over the entire molecule, producing bonding, antibonding, and nonbonding molecular orbitals that contain electrons delocalized across atoms.

This approach provides accurate electronic structures, predicts magnetic properties, and deals well with excited states. However, it is less intuitive for predicting shapes and may require complex computational methods.

Summary of Differences in Electron Localization

• Hybridization (VB): Electrons localized in hybrid orbitals on atoms.
• MO theory: Electrons delocalized in molecular orbitals over entire molecule.
• Hybridization helps visualize bonding but does not represent actual electron distribution per MO theory.

Implications for Chemistry Education and Research

Hybridization remains widely taught due to its simplicity and ability to rationalize molecular geometry rapidly. It is an excellent first approximation for learning molecular shapes, bonding trends, and chemical reactivity.

However, advanced chemistry and research increasingly use molecular orbital theory for quantitative and predictive accuracy, especially in complex molecules and when studying electronic, magnetic, or spectral properties.

Models mixing both approaches, such as Huckel MO theory, demonstrate their complementary strengths. Such hybrid models balance computational simplicity and explanatory power by applying hybridization concepts to sigma bonding and molecular orbitals to pi systems.

Key Takeaways

• Hybridization originates from valence bond theory; it does not exist in pure molecular orbital theory.
• Molecular orbital theory describes electrons as delocalized in molecular orbitals across molecules.
• Hybridization is a useful approximation explaining molecular geometry by combining atomic orbitals into directional hybrids.
• sp3, sp2, and sp hybridizations correspond to tetrahedral, trigonal planar, and linear geometries, respectively.
• Hybrid orbitals have redistributed energies and greater directionality for stronger bonding.
• Molecular orbital theory is more accurate but computationally complex and less intuitive for shape prediction.
• Mixed models like Huckel MO combine hybridization (VB) for sigma bonds and MO theory for pi systems.

Is There Hybridization in MO Theory? Unpacking the Relationship and Reality

Hybridization in Molecular Orbital (MO) Theory does not exist in the traditional sense. It’s a concept born from Valence Bond (VB) theory, not MO theory. This distinction shakes up what many of us learned in chemistry class about orbitals and bonding. So how do these models compare, and can they work together? Let’s dive deep into the chemistry labyrinth and sort fact from handy fiction.

Imagine molecules as social gatherings of electrons. The Valence Bond approach says, “Hey, electrons pair up by mixing their orbitals locally to form hybrids”—think sp3, sp2, and sp types. MO theory, on the other hand, insists that electrons are not stuck in localized ‘hybridized’ orbitals but instead roam freely in molecular orbitals that stretch over the entire molecule. The electrons are far more global party animals than local partners.

Hybridization: A Handy Approximation, Not a Molecular Reality

Hybridization is a brilliant shortcut born from VB theory to explain why molecules have specific shapes — like tetrahedral, trigonal planar, and linear geometries — with bond angles around 109.5°, 120°, or 180°. It pictures atomic orbitals mixing into new orbitals that are equivalent in energy and better oriented to form strong chemical bonds.

However, this idea is not a literal description of how electrons behave. Instead, it is a very useful approximation that makes predicting molecular shapes and reactivity easier. The catch? In MO theory, electrons do not occupy hybrid orbitals; they inhabit molecular orbitals spanning the full molecule.

Think of hybridization as a practical sketch for understanding molecular shape, rather than a true photograph of the electron’s quantum dance. Scientists often joke that chemistry courses are “series of less-egregious lies,” with hybridization sitting comfortably in the “very simple and useful” category of those lies.

Advantages and Limitations: Why Keep Both Models on Your Chemistry Shelf?

The molecular orbital model is the heavyweight champion in predicting electronic behavior accurately. It accounts for properties like magnetic behavior, excitation states, conjugation, and aromaticity very well. However, MO theory is computationally demanding, especially for big molecules—think of it as a super computer trying to solve massive puzzles.

In contrast, the hybridization model is like the chemistry Swiss army knife: simple, accessible, and great for quickly predicting molecular shape—the feature chemists and students often need most. However, it falls short on explaining detailed electronic properties and behaviors like hyperconjugation.

So if hybridization is “not real” but useful, and MO theory is “real” but complicated, why not combine them?

Hybridization Plus MO: The Best of Both Worlds in Huckel MO (HMO) Theory

Here’s where science gets creative. Some models, like Huckel MO theory, marry the VB idea of hybridization (used to describe sigma bonds) with MO theory (used exclusively for pi systems). This hybrid approach explains phenomena such as conjugation and aromaticity better than pure VB theory.

However, even Huckel MO theory, while a big improvement, is still less quantitative than pure MO theory and can miss out on subtleties like hyperconjugation. So the journey for the “perfect” model continues.

Understanding Hybridization Types: A Closer Look

Since we’re busting myths, let’s briefly recall those famous hybridization cases, which remain excellent tools for understanding molecular geometry despite not being fundamental truths in MO theory.

• sp3 Hybridization: Mixing one 2s and three 2p orbitals produces four equivalent sp3 orbitals arranged tetrahedrally at 109.5°. Carbon atoms in methane (CH4) are classic examples.
• sp2 Hybridization: Combines one 2s and two 2p orbitals to form three sp2 orbitals in a trigonal planar arrangement with 120° angles, seen in ethene (C2H4).
• sp Hybridization: Merges one 2s and one 2p orbital to form two linearly arranged sp orbitals with 180° bond angles—like in ethyne (C2H2).

These hybrid orbitals direct bond formation and explain observed molecular shapes well but remember — in MO theory, electrons prefer delocalized molecular orbitals.

Why Does This Matter for Chemistry Students and Researchers?

Understanding that hybridization is an approximation and not a fundamental truth can sharpen your grasp on molecular models and their applications:

1. Better Model Selection: Choose hybridization for rapid shape predictions and MO theory for deep electronic insights, especially in complex molecules.
2. Smoother Learning Curve: Accept hybridization as a stepping stone. It’s okay to start with it before progressing to MO theory for a more nuanced understanding.
3. Recognizing Model Limits: Realize that neither model perfectly captures nature. Each has advantages and blind spots, making chemistry a fascinating balancing act of approximations and reality.

Some Final Thoughts: Chemistry’s Balancing Act

Hybridization in MO theory? Nope—doesn’t really exist. But hybridization itself is too helpful an idea to toss out. It’s like the trusty map you fold and unfold to navigate before you talk to a local or use Google Maps (MO theory) to find the best route.

In the end, MO theory reveals that electrons are the cool kids at the molecular party, spreading their presence across the whole building, not just within localized rooms defined by hybrid orbitals. Meanwhile, hybridization remains the trusty blueprint for structure and bonding, a quick “good enough” guide that keeps chemists out of many jams.

Hybridization is a brilliantly simple tool that helps us understand molecular shapes and bonding trends, but it’s a model with limits—a stepping stone toward the more complex and truthful Molecular Orbital theory. Don’t ditch hybridization just yet. But next time you think electrons live in hybrid orbitals, remember: in MO theory, they’re globetrotting molecular orbitals, and the show is far more interesting.

What is the role of hybridization in Molecular Orbital (MO) theory?

Hybridization is not part of MO theory. MO theory describes electrons in molecular orbitals over the entire molecule. Hybridization arises from valence bond theory as an approximation to explain molecular shapes.

Why is hybridization considered an approximation rather than a reality in chemistry?

Hybridization is a simple model that helps predict molecular shapes. It is not a true description of electron behavior, which is better explained by MO theory. Its usefulness lies in its simplicity, not accuracy.

How does MO theory compare to the hybridization model in predicting molecular properties?

MO theory predicts molecular properties more accurately but struggles with shapes. Hybridization predicts shapes well but is limited beyond that. Each model serves different purposes in chemistry.

Can MO theory and hybridization be combined in chemical models?

Yes. Some models, like Huckel MO theory, mix MO theory with hybridization concepts. They use hybridization for sigma bonds and MO theory for pi bonds to explain phenomena better than pure valence bond theory.

How does hybridization affect bond angles and molecular geometry?

Hybridization mixes atomic orbitals to create new orbitals with specific directions. This leads to characteristic bond angles like 109.5° (sp3), 120° (sp2), and 180° (sp), explaining tetrahedral, trigonal planar, and linear shapes.