Understanding Stoichiometry: A Guide for High School Chemistry Students

Understanding Stoichiometry for High School Chemistry

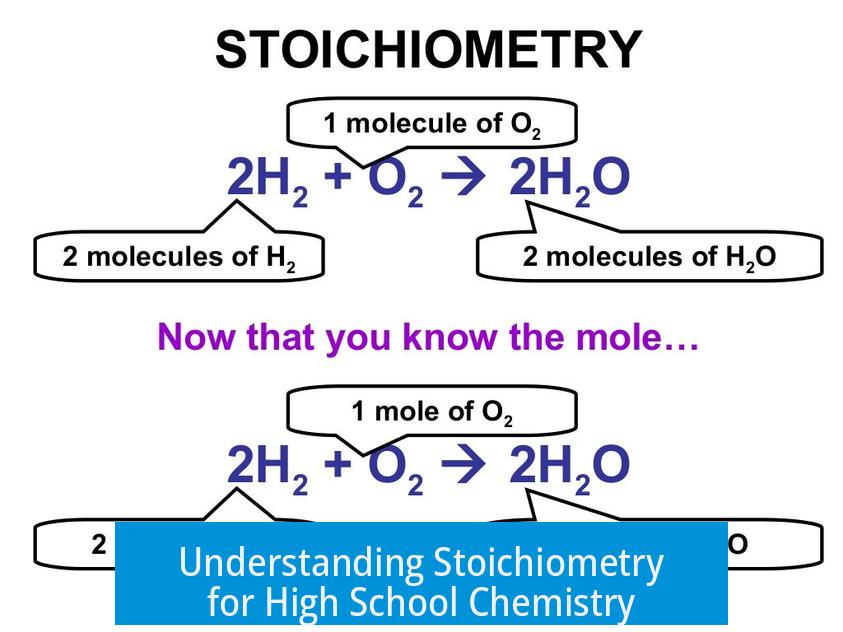
Stoichiometry is the branch of chemistry that deals with calculating the amounts of reactants and products in chemical reactions. At its core, stoichiometry connects the mass of substances to the number of atoms or molecules involved. It enables students to predict how much of each substance is needed or produced in a reaction.

What is Stoichiometry?

Stoichiometry involves the quantitative relationships between the substances in a chemical reaction. Chemical equations show the ratios of molecules or atoms, but practical chemistry requires working with measurable masses.

Since counting each atom or molecule directly is impractical, chemists work with their masses and use the “mole” concept to simplify calculations.

The Mole Concept and Ratios

The mole is a counting unit in chemistry like a dozen but much larger. One mole equals approximately 6.02 x 1023 particles—whether atoms, ions, or molecules.

For example:

• 12 grams of carbon equals 1 mole of carbon atoms.
• 16 grams of oxygen equals 1 mole of oxygen atoms.
• 44 grams of carbon dioxide equals 1 mole of CO2 molecules.

When a chemical formula shows ratios, for instance, one molecule of hydrogen reacting with one molecule of oxygen to form two molecules of water, stoichiometry ensures these ratios apply to moles and masses. So, one mole of hydrogen reacts with half a mole of oxygen to make one mole of water molecules.

Converting Mass to Moles

Stoichiometric calculations often start with converting mass to moles. This requires knowing the molar mass—the mass of one mole of a substance.

Substance	Molar Mass (g/mol)
Hydrogen (H2)	2
Oxygen (O2)	32
Water (H2O)	18

For example, to find the number of moles in 36 grams of water:

1. Find molar mass of water: H (1 g/mol) × 2 + O (16 g/mol) = 18 g/mol
2. Divide given mass by molar mass: 36 g ÷ 18 g/mol = 2 moles

Converting Moles to Mass

The reverse conversion multiplies the moles by the molar mass. For example, 3 moles of water weigh:

• 3 moles × 18 g/mol = 54 grams

Dimensional Analysis in Stoichiometry

Dimensional analysis is a systematic method that treats units like algebraic variables. It helps organize conversions and cancel out units to avoid mistakes.

Each step involves multiplying by conversion factors (ratios) that equal 1 to switch from one unit to another.

For instance, with the mole and molecule relationship:

• 1 mole = 6.022 × 1023 molecules.
• Using this conversion factor allows you to convert molecules to moles or vice versa.

An analogy helps: if a bicycle requires two wheels and one frame, then to build one mole of bicycles, you need two moles of wheels and one mole of frames. Knowing the mass of the wheels lets you find the total mass needed.

Stoichiometry as Unit Conversion

At its heart, stoichiometry is unit conversion. You convert a given known quantity into an unknown one using ratios from balanced equations and molar masses.

This process is similar to converting miles per hour to meters per second:

1. Start with 62 miles per hour.
2. Convert miles to meters (1 mile = 1609 meters).
3. Convert hours to seconds (1 hour = 3600 seconds).
4. Multiply by conversion factors to cancel units and get meters per second.

This approach emphasizes cancellation of units rather than focusing on equal signs. Units on top and bottom cancel out progressively, simplifying the expression.

Applying Stoichiometry Beyond Basic Calculations

Stoichiometry principles extend to concepts like molarity, molality, and gas laws. Understanding how to convert between units and moles is essential in these cases.

Students often find stoichiometry challenging because it involves multiple steps and conversions. Consistent practice and visualizing units can help build confidence.

Summary of Stoichiometry Key Points:

• Stoichiometry connects masses of substances to the number of atoms or molecules through the mole concept.
• The mole is a large counting unit: 6.022 × 1023 particles per mole.
• Convert mass to moles by dividing by molar mass; convert moles to mass by multiplying.
• Dimensional analysis helps manage units to avoid errors and guide conversions.
• Stoichiometry is a form of systematic unit conversion similar to everyday measurements.
• Ratios from balanced chemical equations determine mole and mass relationships between reactants and products.
• Practice and understanding unit cancellations are vital for mastering stoichiometric calculations.

For additional support, students can explore free teaching resources or seek help through online chemistry communities.

What is a mole in stoichiometry and why is it important?

A mole is a counting unit like a dozen but for atoms or molecules. It equals 6.02×10^23 particles. Chemists use moles to count atoms easily because counting individually is impossible.

How do I convert grams to moles in a problem?

Find the molar mass by adding atom weights in the formula. Divide the given grams by this molar mass to get moles. For H2O, 18 grams per mole means 36 grams equals 2 moles.

Why do I need to cancel units during stoichiometry calculations?

Units act like numbers you can cancel out. Canceling units ensures you convert correctly from one measurement to another, like grams to moles or miles per hour to meters per second.

Can you explain stoichiometry using ratios?

Chemical reactions follow ratios. For example, one molecule reacts with two molecules of another. We use moles to keep ratios correct when combining substances in the lab.

How is stoichiometry like everyday unit conversions?

It’s about changing one unit into another, like changing miles/hour to meters/second. You multiply and divide by conversion factors until your units match what you want.

What is the easiest way to master stoichiometry conversions?

Think of units as algebraic terms. Write conversion factors and cancel out units step by step. Practice with simple examples until it feels routine.