Understanding Why Choice A Represents Enantiomers
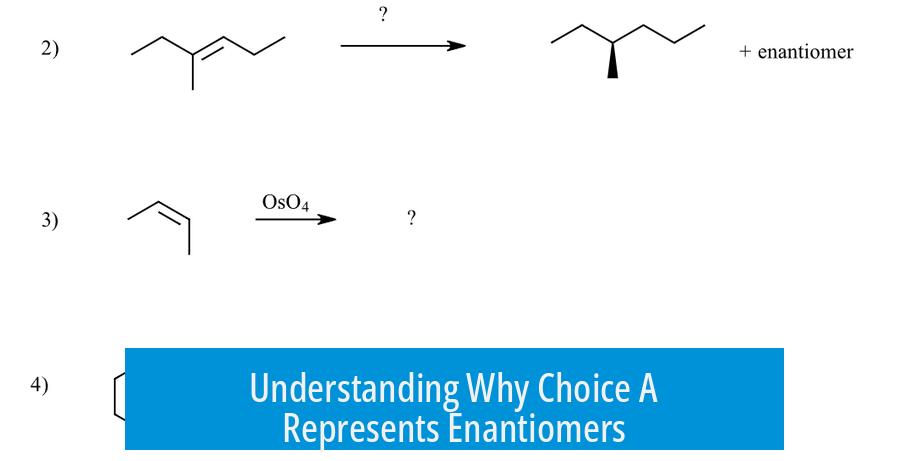
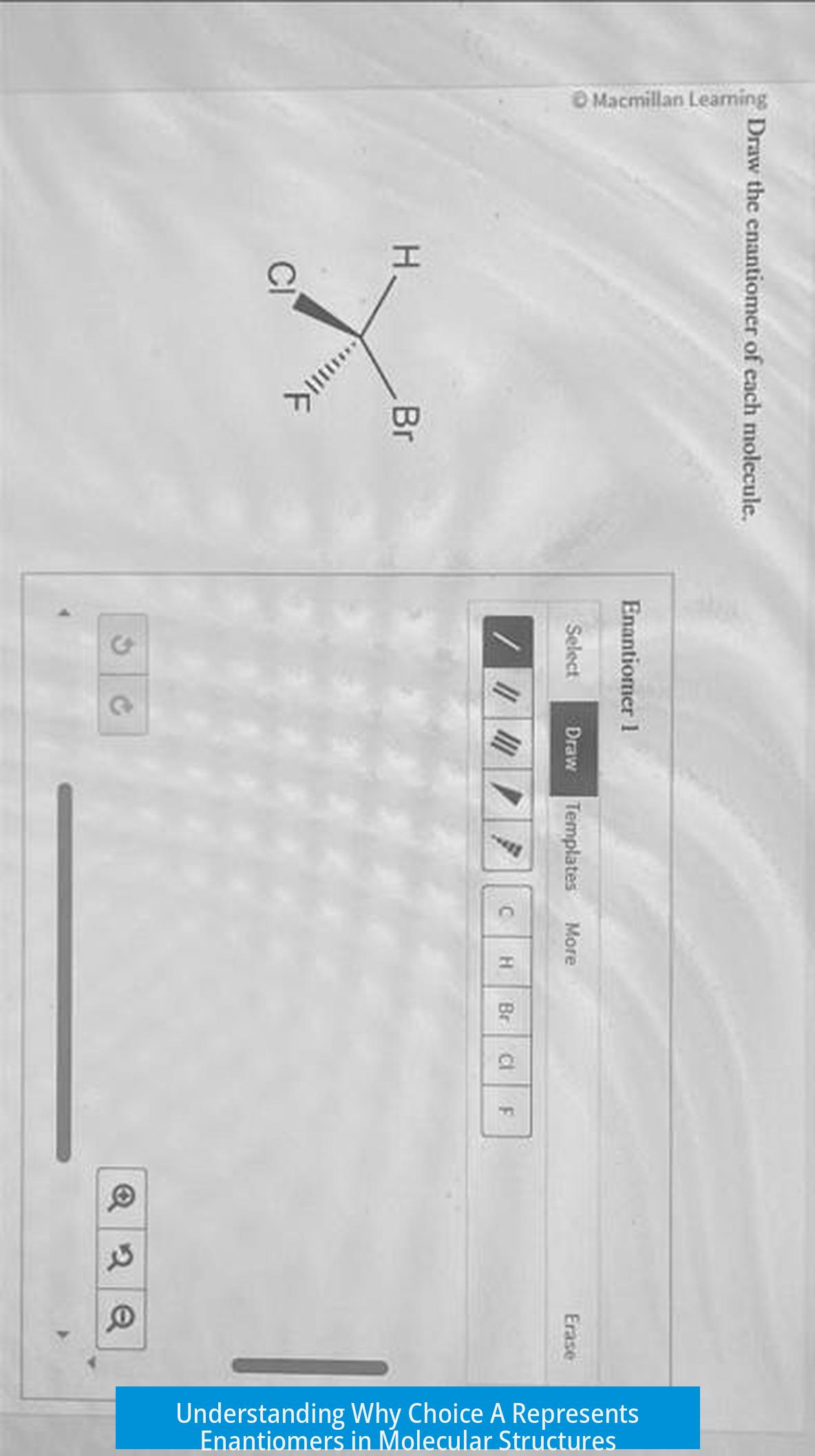
Choice A is the correct answer because it shows molecules that are non-superimposable mirror images, characteristic of enantiomers. Despite initial confusion, this relationship can be clarified by examining the chirality centers and their configurations.
What Defines Enantiomers?
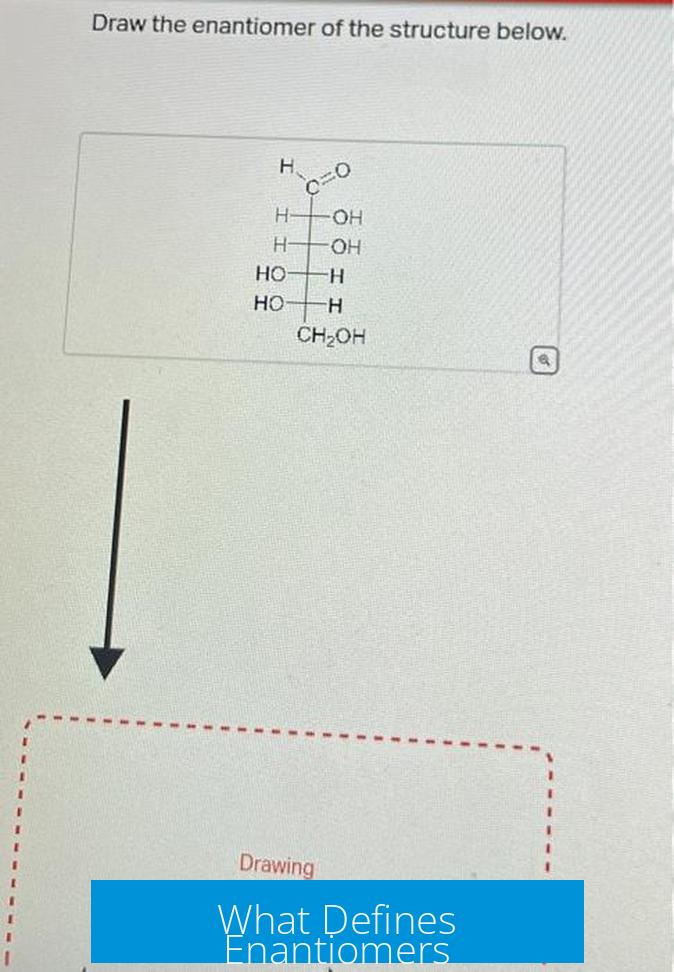
Enantiomers are pairs of molecules that are mirror images but cannot be superimposed. This means they have opposite spatial arrangements around at least one chiral center, making them stereoisomers with distinct R/S configurations.
Visualizing the Mirror Image Relationship

Often, visualizing mirror images in 2D drawings leads to confusion. Even if the structures do not look like direct mirror images at first glance, spatial rotations and assignments reveal this relationship.
- Rotate one molecule 180 degrees along the vertical axis.
- Compare the position of substituents around each chiral center.
This manipulation helps align the molecules conceptually as mirror images.
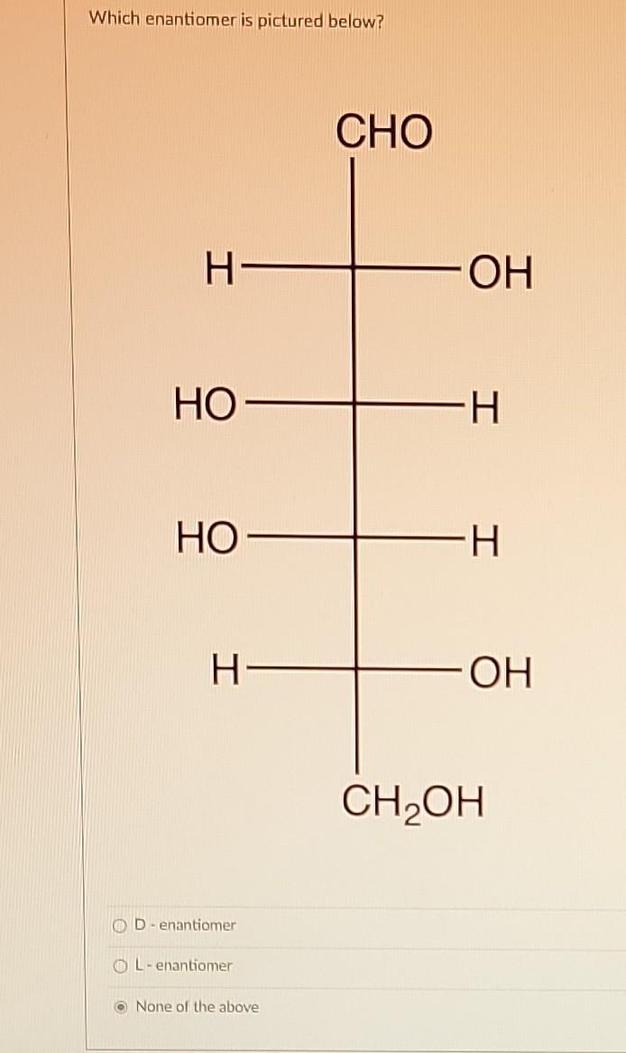
Use of R/S Configuration to Confirm Enantiomerism
Assigning the absolute configuration (R or S) to each chiral center confirms the relationship precisely:
| Molecule | Chiral Center 1 | Chiral Center 2 |
|---|---|---|
| Choice A (Original) | R | S |
| Choice A (Compared Structure) | S | R |
An inversion of all chiral centers’ configurations indicates enantiomerism. This inversion, where every chiral center changes from R to S or S to R, confirms the molecules are mirror images.
Why Other Choices Are Not Enantiomers
- Choice B: Molecules are identical, no mirror image relationship.
- Choice C: Molecules are diastereomers, differing at some but not all chiral centers.
- Choice D: Molecule lacks optical activity and does not have proper chiral centers.
Thus, only choice A meets the strict criteria for enantiomers.
Key Takeaways
- Enantiomers are non-superimposable mirror images with opposite R/S configurations at all chiral centers.
- Visual rotation or assigning R/S configurations helps clarify the mirror image relationship.
- Choice A is correct because it inverts all chiral centers, indicating enantiomerism.
- Other choices represent identical molecules, diastereomers, or non-chiral compounds.
Okay sooooo How Can Choice A, Be the Answer?! Understanding Enantiomers and Mirror Images
The simple answer is: Choice A is the enantiomer because it is the non-superimposable mirror image of the original molecule, even if it doesn’t look like one at first glance. Sometimes visualizing molecules can be tricky, and what you see initially might not tell the full story. Let’s break down why choice A fits the bill, despite looking suspicious.
Enantiomers are kind of like odd socks—they look similar and related but can’t be perfectly matched up one on one. By definition, enantiomers are non-superimposable mirror images. This means if you put one molecule in front of a mirror, what you see on the other side is its enantiomer, but you can’t flip or rotate one to make it look exactly like the other.
Why Does Choice A Confuse Us?
You point out a great observation: choice A does have chiral centers with inverted groups, but it doesn’t scream “mirror image” at first glance. That’s normal. Not every mirror image looks obvious without some manipulation. Chemically, what counts is that all chiral centers invert their configuration in enantiomers.
So, how do we verify? There’s a neat trick: assign the R/S configuration to each chiral center. Think of R and S as “right” and “left” handedness for each carbon.
Assigning R/S Configurations, the Key to Seeing the Mirror
- Take choice A and assign R/S to all the chiral carbons.
- Do the same for the original molecule.
- If all of the chiral centers have the opposite designation (R becomes S and vice versa), they are mirror images.
By doing this, you see choice A’s centers are inverted relative to the original molecule—this confirms that choice A is indeed the mirror image, aka the enantiomer.
It sounds a bit like decoding a secret message. But once you get that each chiral center flips, it’s crystal clear. Choice A is the true mirror twin.
Visualizing the Mirror: Rotate to Complicate, Rotate to Clarify
Still struggling with “mirror image” feelings? Here’s a cool mental exercise:
- Imagine grabbing the molecule on the right and rotating it 180 degrees left to right.
- Watch carefully. You just gave yourself a new viewpoint.
- In this new orientation, you’ll see the configuration matches that of the molecule on the left but flipped at every chiral center.
This visualization helps chemists confirm mirror images without relying solely on guessing or eyeballing it. Rotation is the key to unlocking symmetry puzzles.
Substituent Swap Magic: Why Exchanging Two Groups Creates a Mirror Image
Another rule helps here: swapping two substituents on a chiral carbon creates the mirror image. This is like flipping left and right hands. One swap turns the molecule’s “handedness” inside out.
Since choice A involves this inversion of groups on its chiral centers, it matches the mirror image definition perfectly. Despite appearances, the molecule’s handedness changes, making it a proper enantiomer.
What About the Other Choices? Why Are They Not Right?
| Choice | Why It’s Not an Enantiomer |
|---|---|
| B | Two molecules are identical. No mirror image difference here, so definitely not enantiomers. |
| C | They are diastereoisomers. These are stereoisomers that are not mirror images and differ at some, but not all, chiral centers. |
| D | Not optically active. Without chirality or inverse configurations, no enantiomeric relationship exists. |
So, a quick cheat sheet: Choice A = enantiomer; B = identical; C = diastereoisomer; D = achiral.
Let’s Recap: Why Choice A Wins the Crown
- Enantiomers must be non-superimposable mirror images.
- Assigning R/S configurations to choice A shows all chiral centers are opposite compared to the original.
- Rotating molecules helps “see” the mirror relationship when it’s not obvious.
- Group swaps at chiral carbons produce mirror images — a key concept demonstrated by choice A.
- Other choices falter on identity, partial difference, or lack of chirality.
In conclusion, choice A fits the very criteria for enantiomers, even if your eyes need a little help to catch what the molecule is doing. Chemistry loves to sneak in hidden tricks like this. It’s like molecular magic: the two look similar but their handedness sets them apart completely.
Bonus: Practical Tip for Students and Chemists
Feeling stuck next time? Don’t just trust what your eyes say. Always assign R/S configurations on all chiral centers. This method cuts through confusion and settles debates like “Is this a mirror image or not?” faster than debates on which coffee to choose.
Also, model kits or 3D visualization software can be lifesavers. Rotate, flip, and swap groups virtually to see the right answer unfold. Don’t worry if it initially confuses you—that’s normal and part of the learning curve.
So, are you ready to tackle your next stereochemistry puzzle with confidence? Remember, seeing is believing—but R/S assignments are the proof.
Why does choice a qualify as an enantiomer if it doesn’t look like a mirror image?
Choice a has chiral centers with groups inverted. By assigning R and S configurations, you see they are opposite, which means they are mirror images even if it’s hard to visualize directly.
How can R/S configuration assignments help prove that two molecules are enantiomers?
Assigning R or S to each chiral center shows if configurations are opposite. Opposite R/S at all centers confirms a non-superimposable mirror image, defining enantiomers.
Is rotating the molecule necessary to identify enantiomers?
Yes. If you rotate one molecule 180 degrees, you can better visualize the mirror image relationship. If unsure, rely on R/S assignments to confirm.
What distinguishes enantiomers from diastereomers in this context?
Enantiomers are non-superimposable mirror images with all chiral centers inverted. Diastereomers differ at some but not all chiral centers and are not mirror images.
Why is choice b not an enantiomer in this example?
Choice b represents identical molecules, not mirror images. They have the same configuration, so no inversion occurs. Therefore, they are not enantiomers.



Leave a Comment