How the Number of Electrons in an Electron Shell is Determined: Key Principles and Calculations

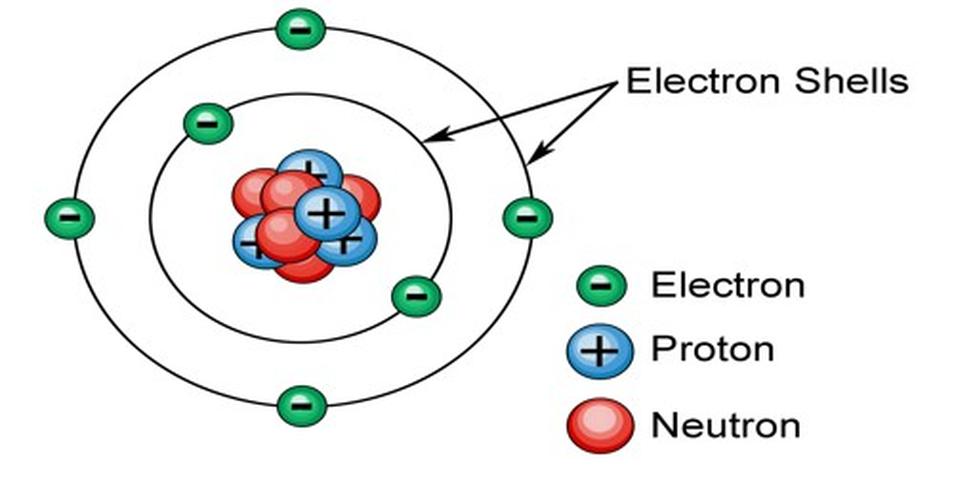
How is the Number of Electrons in an Electron Shell Determined?

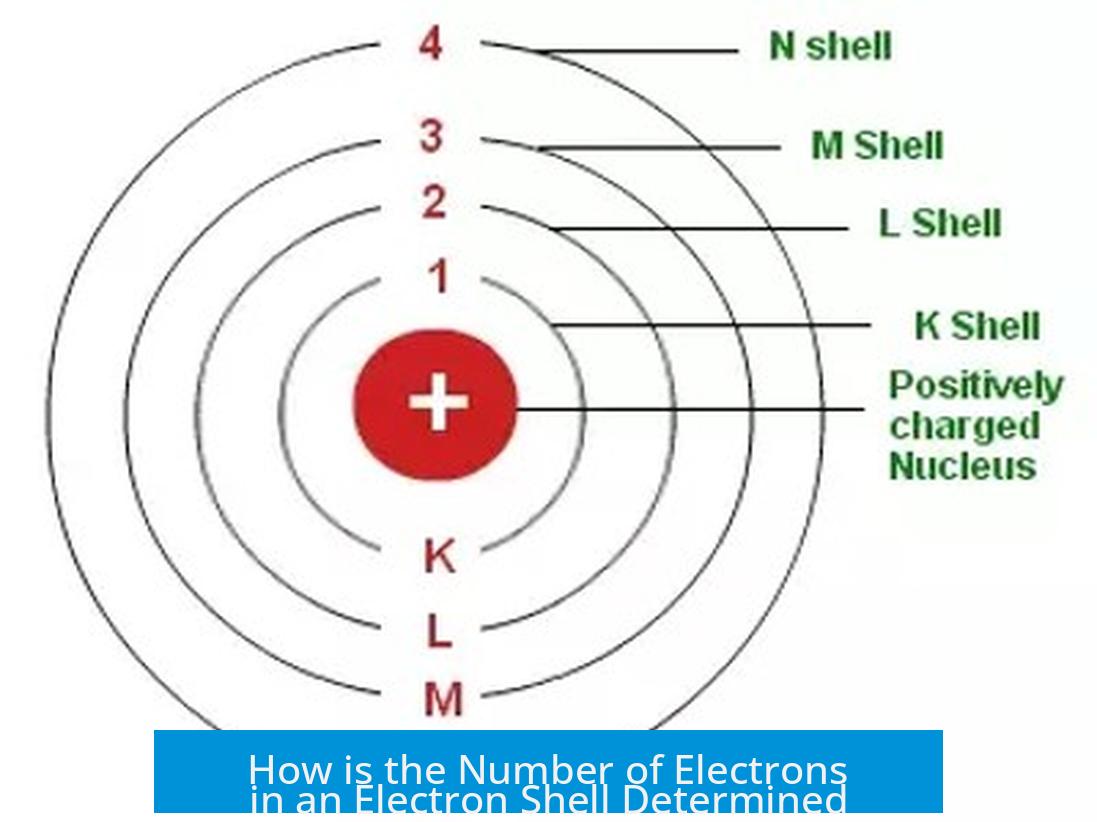
The number of electrons in an electron shell is determined by the quantum mechanical principles governing electron configurations, specifically the quantum numbers (n, l, ml, ms) and the Pauli exclusion principle, which together define the number of available orbitals and how many electrons each can hold.

This arrangement follows a precise mathematical and physical framework that controls the behavior and distribution of electrons around an atomic nucleus.

1. Understanding Quantum Numbers

Each electron in an atom is described by four quantum numbers. These numbers define the electron’s state, including which shell and subshell it occupies and the electron’s spin orientation. They establish the rules that regulate how many electrons can populate any given shell.

1.1 Primary Quantum Number (n)

• Represents the electron’s main energy level or shell.
• Can only take positive integer values: 1, 2, 3, and so forth.
• The larger the value of n, the higher the energy level and the greater the distance of the electron from the nucleus.

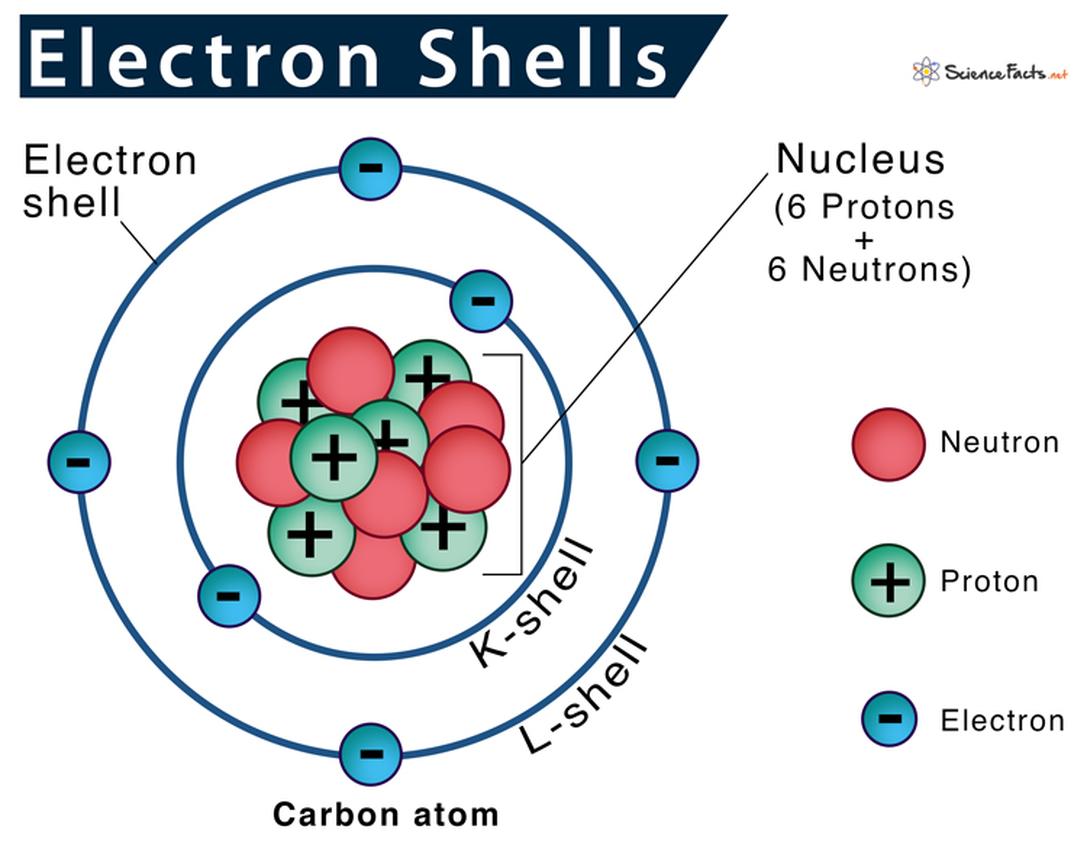
For example, when n = 3, this corresponds to the third electron shell.

1.2 Angular Momentum Quantum Number (l)

• Specifies the subshell type (orbital shape) within a shell.
• Possible values range from 0 to n – 1.
• Determines the type of orbital: s (l=0), p (l=1), d (l=2), or f (l=3).

For n = 3, the allowed l values are 0, 1, and 2, corresponding to 3s, 3p, and 3d subshells respectively.

1.3 Magnetic Quantum Number (ml)

• Defines the specific orbital within a subshell.
• The values range from -l to +l, including zero.
• The total number of orbitals in a subshell equals 2l + 1.

For a d subshell (l = 2), the possible ml values are -2, -1, 0, 1, 2, equaling 5 orbitals in total.

1.4 Spin Quantum Number (ms)

• Represents the intrinsic spin of an electron.
• May be +1/2 or -1/2.
• Allows each orbital to hold two electrons with opposite spins.

2. The Pauli Exclusion Principle

The Pauli exclusion principle states that no two electrons in an atom can share identical sets of all four quantum numbers.

This principle restricts the occupancy of orbitals to a maximum of two electrons, each with opposite spins.

Consequently, each orbital holds at most two electrons.

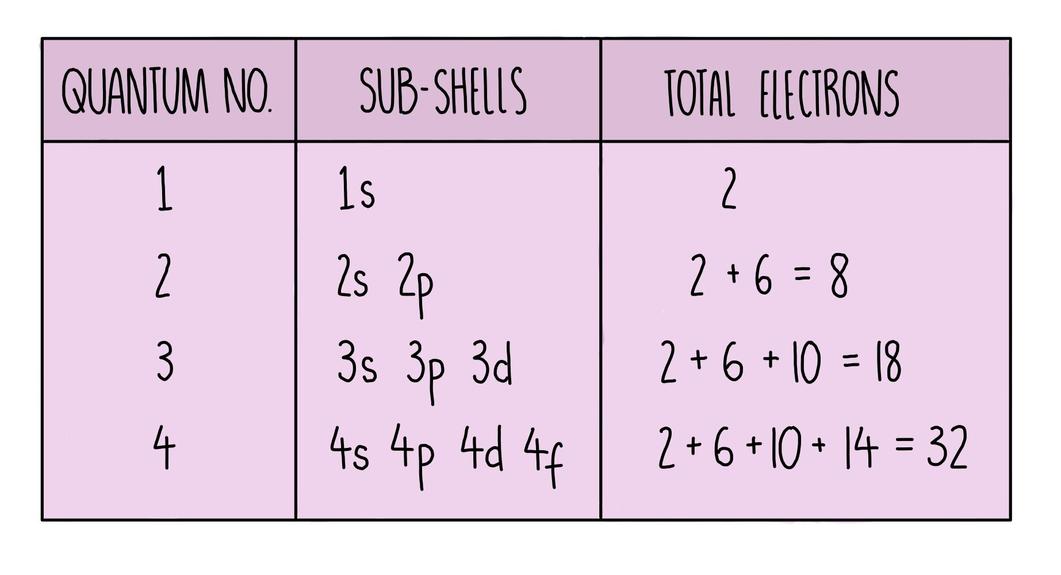
3. Calculating Electron Capacity for Subshells and Shells

The combination of allowed orbitals and the Pauli principle leads to a quantifiable limit on electron numbers per subshell and shell.

Subshell Type (l)	Number of Orbitals	Max Electrons per Subshell
s (0)	1	2
p (1)	3	6
d (2)	5	10
f (3)	7	14

The total electrons in a shell consist of the sum of electrons across all subshells for that shell. For instance, at n = 3:

• 3s: 1 orbital × 2 electrons = 2 electrons
• 3p: 3 orbitals × 2 electrons = 6 electrons
• 3d: 5 orbitals × 2 electrons = 10 electrons

Total possible electrons in the third shell = 2 + 6 +10 = 18 electrons.

4. Electron Filling Order and Energy Considerations

Electrons fill orbitals starting from the lowest energy levels to higher ones, adhering to the quantum rules.

Although the principal quantum number designates shells, actual energy levels influence filling. Electrons typically fill n = 1, then n = 2, before occupying n = 3. The 4s subshell fills before 3d due to energy order, but each shell follows the quantum number rules for electron accommodation.

5. Physical Laws Determining Electron Numbers

The regular pattern of electron numbers per shell arises from quantum mechanics. The wave-like properties of electrons impose discrete energy levels and orbital shapes.

Experimental and theoretical studies show electrons must occupy allowed quantum states without duplication, constrained by the Pauli exclusion principle.

These laws combine to produce the orderly, predictable limits on how many electrons an electron shell can contain.

Summary of Key Points

• Electron shells are defined by the primary quantum number n.
• Subshells within shells correspond to different angular momentum quantum numbers l.
• Each subshell contains a fixed number of orbitals determined by the magnetic quantum number ml.
• Each orbital can hold up to two electrons with opposite spins (ms) due to the Pauli exclusion principle.
• The total number of electrons in a shell is the sum of electrons across all its subshells.
• Electron filling proceeds by increasing energy levels governed by these quantum rules.
• The whole system is a result of fundamental quantum mechanical laws that restrict electron configurations strictly.

How Is the Number of Electrons in an Electron Shell Determined?

Simply put, the number of electrons in an electron shell is determined by how many unique quantum states that shell can hold, governed by the four quantum numbers and the Pauli exclusion principle. This establishes a precise count of electrons each shell can accommodate—no more, no less. Let’s unpack this quantum puzzle and see how nature manages to keep things so orderly inside atoms.

Have you ever wondered why electrons don’t just crowd into one spot like guests at an all-you-can-eat buffet? The answer lies deep in quantum mechanics. Electrons are picky; they like to have their own distinct “address” in the atom, and these addresses are encoded by quantum numbers. Understanding these numbers is the key to figuring out our question.

Quantum Numbers: The Electron’s ID Card

Every electron has four numbers that define its state. Think of them as coordinates on a map:

• Primary quantum number (n) – This one tells which energy level or shell the electron belongs to. n takes only whole positive integers like 1, 2, 3, etc. The higher the n, the further from the nucleus and the more energetic the electron.
• Angular momentum quantum number (l) – This defines the type of subshell or shape of the orbital inside that shell: s, p, d, or f. The value ranges from 0 up to n-1.
• Magnetic quantum number (ml) – It specifies the orientation of the orbitals within a subshell and runs from -l to +l. This number indicates how many orbitals of a given type exist.
• Spin quantum number (ms) – Electrons have spin, either +1/2 or -1/2. This affects how electrons pair up within orbitals.

These quantum numbers set the stage. If electrons are guests, then the quantum numbers make sure nobody shares the exact seat.

Pauli Exclusion Principle: The Electron Bouncer

Imagine a club with strict guest rules. The Pauli exclusion principle kicks in here: no two electrons can have the exact same set of quantum numbers at the same time. Since ms has two options, each orbital can host a maximum of two electrons that spin differently.

This simple rule limits how many electrons can squeeze into each orbital: only two, spinnin’ in opposite directions.

Counting Electrons per Subshell and Shell

The magic math behind electron counting comes down to orbitals and their spin limits. The number of orbitals in each subshell is determined by ml values, and since each orbital holds two electrons, let’s do some quick arithmetic:

Subshell (l)	Number of Orbitals (2l + 1)	Max Electrons (Orbitals × 2)
s (l=0)	1	2
p (l=1)	3	6
d (l=2)	5	10
f (l=3)	7	14

So, if you take shell number n=3 as an example, it comprises subshells s, p, and d.

• 3s: 1 orbital → 2 electrons.
• 3p: 3 orbitals → 6 electrons.
• 3d: 5 orbitals → 10 electrons.

Totaling to a maximum of 18 electrons for shell 3.

Why Does This Matter? The Why Behind the Pattern

Someone might ask, “Why this neat arrangement? Could electrons just break the rules and pile up?” The simple answer: physics. The quantum mechanical laws ensure electrons fill shells based on energy levels, seeking stability. Electrons fill the lowest energy shell (n=1) first, then move outward (n=2, n=3, and so forth).

However, electrons don’t fill shells purely in order of n. 4s fills before 3d due to subtle energy considerations—a quirk that, while fascinating, is a story for another time.

What Does This Tell Us About Electron Arrangements?

From the quantum numbers to the fundamental Pauli exclusion principle, the number of electrons in a shell isn’t random. It’s a consequence of quantum mechanics acting as a strict but fair rulebook. This rulebook defines orbital shapes, how many orbitals exist, and how electrons spin, packing atoms efficiently and predictably.

For anyone interested in chemistry or physics, this knowledge explains the architecture of the periodic table, how elements bond, and why atoms behave the way they do.

Practical Tips for Visualizing This Entire Framework

1. Remember each electron has a four-number address: n, l, ml, ms.
2. Use the formula Number of orbitals = 2l + 1 to find orbitals per subshell.
3. Multiply orbitals by 2 for max electrons (thanks, electron spin!).
4. Add across all subshells in a shell for total capacity.
5. Think of filling shells starting at n=1 and moving outwards.

By following these steps, you can calculate how many electrons live in each shell without breaking a sweat.

The Big Takeaway

The number of electrons in an electron shell mirrors the number of unique quantum states electrons can occupy, as dictated by quantum numbers and the Pauli exclusion principle. This ensures atoms stay balanced and allows chemists to predict element properties with confidence.

Next time you glance at the periodic table, remember: behind each element lies a finely tuned quantum code balancing electrons like guests at a perfectly arranged banquet, with every electron having its unique seat at the atomic table.

How do quantum numbers determine the number of electrons in a shell?

The primary quantum number (n) sets the shell’s energy level. The angular momentum quantum number (l) defines subshell types (s, p, d, f). The magnetic quantum number (ml) shows the number of orbitals. Each orbital holds up to 2 electrons, defining total electrons per shell.

Why can each orbital contain only two electrons?

The Pauli exclusion principle states no two electrons can share the same set of quantum numbers. Since the spin quantum number (ms) has two possible values (+1/2 or -1/2), an orbital can hold only two electrons with opposite spins.

How is the maximum number of electrons in a subshell calculated?

The number of orbitals in a subshell is 2l + 1, where l is the angular momentum number. Each orbital holds 2 electrons, so electrons per subshell equal 2 × (2l + 1). For example, a d subshell (l=2) has 5 orbitals and 10 electrons max.

What determines the total electrons in an electron shell?

The shell’s total electrons add the maximum electrons of all its subshells. For instance, at n=3, subshells s, p, and d hold 2, 6, and 10 electrons respectively, summing to 18 electrons for that shell.

How does electron filling order affect electron distribution in shells?

Electrons fill shells from low to high energy levels (n=1 before n=2, etc.). Each shell fills according to its subshell capacity and quantum rules, which governs the order and number of electrons per shell.