Why Can There Only Be Two Electrons in the First Orbital? A Look at Quantum Numbers and the Pauli Exclusion Principle

Why Can There Only Be Two Electrons in the First Orbital?

The fundamental reason only two electrons can occupy the first orbital (1s) is due to the Pauli Exclusion Principle, which states that no two electrons can share the exact same set of four quantum numbers. Since the 1s orbital fixes three quantum numbers, the only variable is the electron spin, which has two possible values, thus limiting the orbital capacity to two electrons.

Quantum Numbers and Electron Occupancy

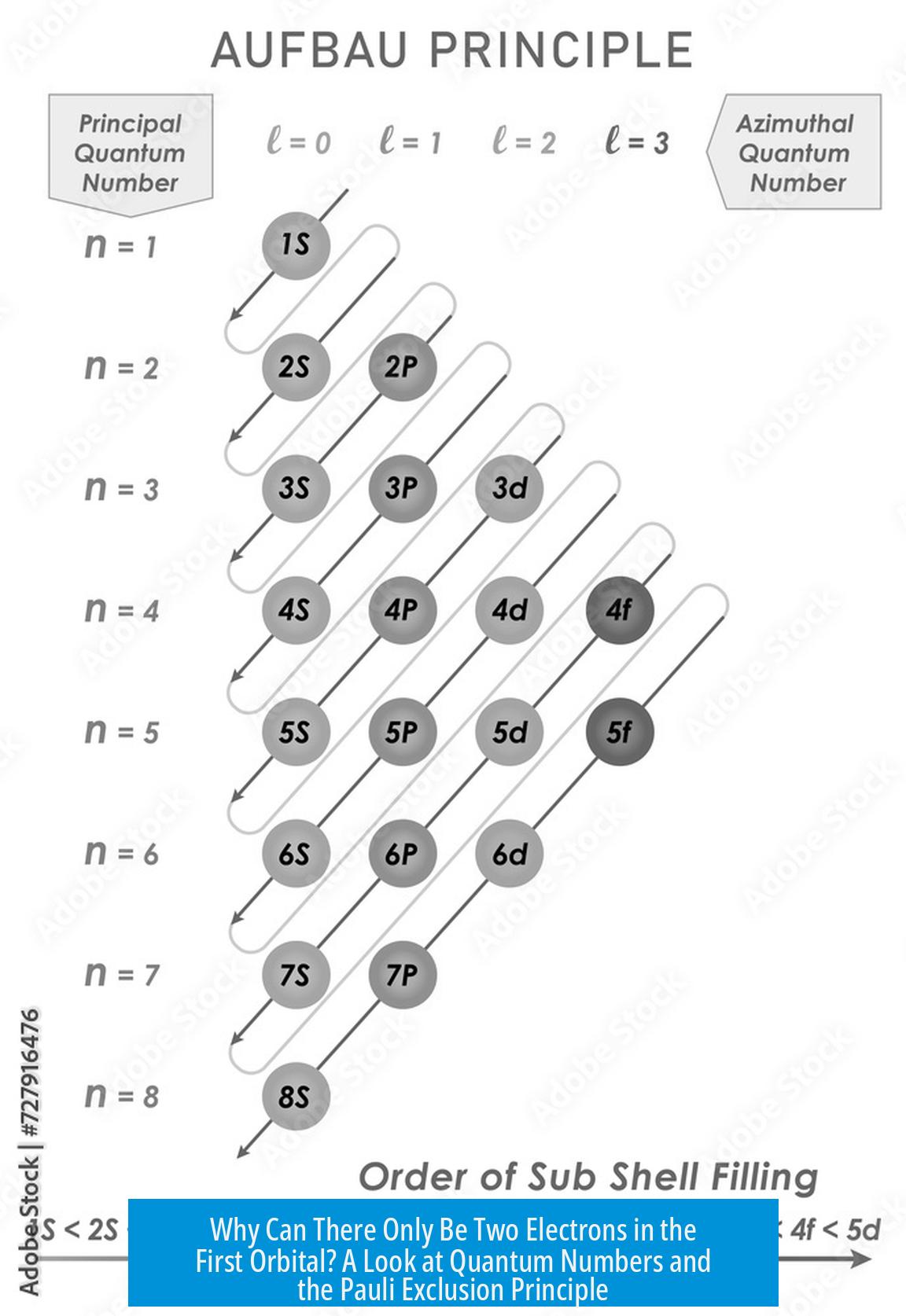
Electrons in atoms are described by four quantum numbers. These numbers specify the energy state, shape, orientation, and spin of each electron. They are:

• Principal quantum number (N): This defines the shell or energy level (N = 1, 2, 3,…).
• Azimuthal quantum number (L): Defines the subshell or orbital type (s, p, d, f…), with values from 0 up to N-1.
• Magnetic quantum number (Ml): Specifies the orientation of the orbital within a subshell; values range from -L to +L.
• Spin quantum number (Ms): Describes the intrinsic spin of the electron; it can be either +1/2 or -1/2.

In the first orbital (1s), these numbers take the values N=1, L=0, Ml=0. Only the spin quantum number varies between the two electrons, meaning there are only two unique quantum states possible.

Pauli Exclusion Principle and Its Implications

The Pauli Exclusion Principle demands that no two electrons in the same atom can have identical quantum numbers. This principle enforces a strict limit on how many electrons can fill any given orbital.

• For the 1s orbital, since quantum numbers N, L, and Ml are fixed, only two electrons can occupy it—each with opposite spins (+1/2 or -1/2).
• A third electron attempting to enter this orbital would necessarily share a quantum state with one of the existing electrons, violating the Pauli principle.

Electron Spin and Orbital Filling

Electron spin plays a critical role in orbital occupancy. It does not reflect physical spinning but is an intrinsic property:

• Spin has two orientations: +1/2 and -1/2.
• Oppositely spinning electrons can pair up in one orbital, reducing energy through exchange interaction.
• This pairing explains why two electrons fit in one orbital and why a third cannot join without breaking fundamental quantum rules.

Orbital Structure and Shell Distribution

The first electron shell (N=1) contains a single 1s orbital. This shell lies closest to the nucleus, where electrons experience strong electrostatic attraction to the positively charged nucleus.

• Because of this proximity and quantum mechanical constraints, the first shell supports only one orbital.
• Subsequent shells have more orbitals: the second shell (N=2) contains four orbitals (one 2s and three 2p orbitals), the third shell (N=3) has nine orbitals, and so forth.
• Outer shells are larger and experience less nuclear attraction, allowing for more orbitals and electrons.

Quantum Mechanical Foundation: Wavefunction Antisymmetry

Electrons are fermions with half-integer spin. Their quantum state is described by a wavefunction that must be antisymmetric with respect to the exchange of any two electrons.

• Swapping two electrons changes the sign of the wavefunction: Ψ(1,2) = -Ψ(2,1).
• If two electrons shared identical quantum states, the wavefunction would equal its own negative, forcing it to zero.
• This cancellation means such a state cannot physically exist and enforces the Pauli Exclusion Principle.
• Electrons differ in spin orientation when occupying the same orbital, preventing wavefunction cancellation.

Conceptual Analogies to Understand Orbital Filling

While the laws are quantum mechanical and abstract, analogies help visualization:

• Imagine orbitals as petals around a flower’s center (the nucleus). Near the center, space is limited, so the number of petals (orbitals) is few, and each can hold only two electrons.
• Electron repulsion pushes additional electrons to outer shells, which have more petals and room.
• Opposite spins allow two electrons to share a petal (orbital), but identical spins repel and prevent a third electron from fitting.

Summary of Key Points

• The Pauli Exclusion Principle limits the first orbital (1s) to two electrons.
• Three quantum numbers in a 1s orbital are fixed; only spin varies to differentiate electrons.
• Spin can be +1/2 or -1/2, allowing precisely two unique electron states per 1s orbital.
• Wavefunction antisymmetry forbids identical electron states, precluding more than two electrons per orbital.
• The first shell has one orbital due to strong nuclear attraction and quantum restrictions.
• Electron repulsion and space constraints drive additional electrons into outer orbitals.

Why does the first orbital only hold two electrons?

The first orbital, called 1s, can hold two electrons because of the Pauli exclusion principle. It allows only two electrons with opposite spins, giving two unique sets of quantum numbers.

How do quantum numbers limit electron occupancy in the first orbital?

Electrons are described by four quantum numbers. In the 1s orbital, three numbers are fixed, and only the spin quantum number differs (+1/2 or -1/2). This limits the orbital to two electrons.

What role does electron spin play in occupying the first orbital?

Electron spin can be +1/2 or -1/2. Paired electrons in the same orbital must have opposite spins, allowing exactly two electrons and preventing a third with the same spin state.

Why can’t a third electron enter the first orbital?

A third electron would share the same quantum numbers as one of the others, violating the Pauli exclusion principle. This causes the wavefunction to cancel and forbids the third electron.

Is the size or space in the first orbital why only two electrons fit?

No, the limitation arises from quantum rules and wavefunction antisymmetry, not physical size or electron repulsion. The first shell has one orbital, and its capacity is set by quantum mechanics.